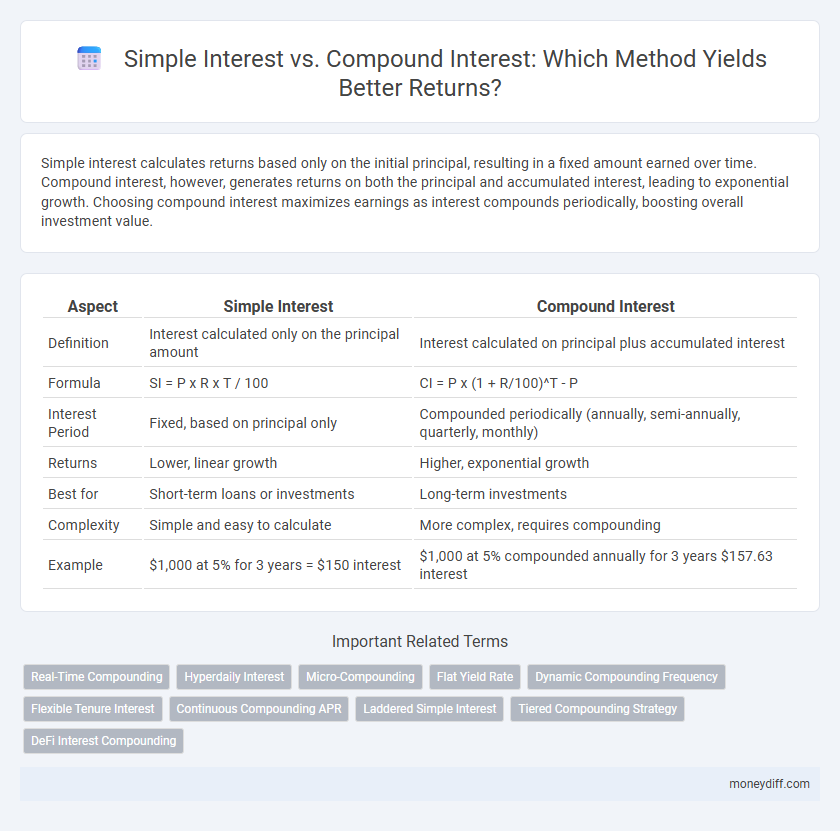
Simple interest calculates returns based only on the initial principal, resulting in a fixed amount earned over time. Compound interest, however, generates returns on both the principal and accumulated interest, leading to exponential growth. Choosing compound interest maximizes earnings as interest compounds periodically, boosting overall investment value.
Table of Comparison
| Aspect | Simple Interest | Compound Interest |
|---|---|---|
| Definition | Interest calculated only on the principal amount | Interest calculated on principal plus accumulated interest |
| Formula | SI = P x R x T / 100 | CI = P x (1 + R/100)^T - P |
| Interest Period | Fixed, based on principal only | Compounded periodically (annually, semi-annually, quarterly, monthly) |
| Returns | Lower, linear growth | Higher, exponential growth |
| Best for | Short-term loans or investments | Long-term investments |
| Complexity | Simple and easy to calculate | More complex, requires compounding |
| Example | $1,000 at 5% for 3 years = $150 interest | $1,000 at 5% compounded annually for 3 years $157.63 interest |
Understanding Simple Interest: The Basics
Simple interest calculates returns based only on the original principal, using a fixed percentage rate over a defined period, making it straightforward and predictable. The formula SI = P x R x T / 100 is commonly used, where P is the principal amount, R is the annual interest rate, and T is the time in years. This method is ideal for short-term loans or investments where the interest amount does not compound or accumulate on the previously earned interest.
What Is Compound Interest? A Brief Overview
Compound interest is the process of earning interest on both the initial principal and the accumulated interest from previous periods, leading to exponential growth of investments over time. It differs from simple interest, which calculates interest solely on the original principal amount, resulting in linear growth. The frequency of compounding--such as annually, semi-annually, or quarterly--directly impacts the total returns, making compound interest a powerful tool for maximizing long-term investment gains.
Key Differences Between Simple and Compound Interest
Simple interest calculates returns based solely on the original principal amount, resulting in linear growth over time. Compound interest, however, generates earnings on both the initial principal and the accumulated interest, causing exponential growth. This key difference means compound interest typically yields higher returns over long periods compared to simple interest.
The Mathematical Formulas: Simple vs Compound
Simple interest is calculated using the formula I = P x r x t, where I is the interest, P is the principal, r is the annual interest rate, and t is the time in years. Compound interest is determined with the formula A = P(1 + r/n)^(nt), where A is the amount, P is the principal, r is the annual interest rate, n is the number of times interest is compounded per year, and t is the time in years. The key difference lies in compound interest's exponential growth due to interest on interest, compared to simple interest's linear growth.
Real-Life Examples: Simple Interest in Practice
Simple interest is commonly used in short-term loans or car financing where the interest is calculated only on the principal amount, resulting in predictable and straightforward payments. For example, a $10,000 auto loan at 5% simple interest over three years generates $1,500 in interest without compounding effects. This real-life application makes simple interest ideal for budgeting fixed returns and understanding total repayment costs upfront.
Compound Interest in Action: How It Works
Compound interest calculates returns by reinvesting earned interest, allowing the principal to grow exponentially over time. Unlike simple interest, which only applies to the original principal, compound interest generates earnings on both initial capital and accumulated interest. This effect accelerates wealth growth, making compound interest a powerful tool for long-term investments.
Which Grows Faster? A Comparison of Returns
Compound interest grows faster than simple interest because it calculates returns on the initial principal plus accumulated interest, resulting in exponential growth. Simple interest only applies to the principal, leading to linear returns over time. Over longer periods and higher interest rates, compound interest significantly outperforms simple interest in total returns.
When to Use Simple Interest vs Compound Interest
Simple interest is ideal for short-term loans or investments where the principal amount remains constant, such as personal loans or car financing. Compound interest is best suited for long-term investments or savings accounts because it calculates interest on both the principal and accumulated interest, maximizing returns over time. Understanding the time horizon and the nature of the financial product helps determine whether simple or compound interest will yield better growth.
Pros and Cons: Evaluating Each Method
Simple interest provides straightforward calculations and predictable returns, making it ideal for short-term investments or loans where clarity is essential. Compound interest, with its ability to generate earnings on both principal and accumulated interest, offers the advantage of exponential growth, particularly beneficial for long-term investments. However, compound interest involves more complex calculations and may accrue higher costs on debts, while simple interest lacks the power of reinvested growth but remains easier to manage and understand.
Choosing the Right Strategy for Your Financial Goals
Simple interest calculates returns on the principal amount only, making it suitable for short-term investments with predictable growth. Compound interest reinvests earnings, generating exponential growth ideal for long-term financial goals and wealth accumulation. Selecting between simple and compound interest depends on your investment horizon and desired return strategy for maximizing financial outcomes.
Related Important Terms
Real-Time Compounding
Simple interest calculates returns based solely on the original principal, resulting in linear growth over time, whereas compound interest generates exponential growth by reinvesting earned interest at regular intervals, maximizing real-time compounding benefits. Real-time compounding accelerates wealth accumulation by continuously adding interest to the principal, significantly outperforming simple interest in long-term investment scenarios.
Hyperdaily Interest
Hyperdaily interest calculates returns by compounding interest multiple times within a single day, significantly amplifying earnings compared to simple interest, which applies a fixed rate on the principal only. This method leverages the exponential growth effect of compound interest, ensuring higher returns over short periods due to frequent interest compounding cycles.
Micro-Compounding
Simple interest calculates returns based solely on the principal amount, resulting in linear growth over time, whereas compound interest, especially micro-compounding, reinvests interest earned continuously or at very short intervals, leading to exponential growth of the investment. Micro-compounding maximizes returns by frequently adding accrued interest back to the principal, significantly increasing the amount earned compared to standard compounding periods.
Flat Yield Rate
Simple interest calculates returns using a flat yield rate applied only to the original principal, resulting in linear growth over time. Compound interest reinvests earnings, producing exponential growth by applying the flat yield rate to the accumulated amount, including prior interest.
Dynamic Compounding Frequency
Dynamic compounding frequency significantly enhances returns by adjusting the interval at which interest is compounded, unlike simple interest which calculates returns linearly without reinvesting interest. Increasing compounding frequency from annually to monthly or daily exponentially accelerates growth, maximizing investment potential through continuous accumulation of earned interest.
Flexible Tenure Interest
Simple interest calculates returns using a fixed percentage on the principal amount over a flexible tenure, making it straightforward but less lucrative for longer periods. Compound interest, however, reinvests the earned interest at regular intervals during the flexible tenure, resulting in exponentially higher returns compared to simple interest.
Continuous Compounding APR
Simple interest calculates returns based on the initial principal and a fixed rate over time, whereas compound interest, especially with continuous compounding APR, exponentially grows returns by reinvesting earnings at every possible moment. Continuous compounding APR uses the formula A = Pe^(rt), maximizing investment growth beyond standard compound intervals.
Laddered Simple Interest
Laddered simple interest involves investing in multiple fixed-term deposits with staggered maturity dates, allowing periodic access to principal while earning straightforward, predictable interest calculated on the original principal only. This approach contrasts with compound interest, which reinvests earned interest, resulting in exponential growth but less liquidity and more complexity in return calculations.
Tiered Compounding Strategy
Simple interest calculates returns based solely on the principal amount, resulting in linear growth, whereas compound interest generates exponential growth by reinvesting earned interest. A tiered compounding strategy enhances returns by applying different compounding frequencies or rates at various stages, optimizing overall investment growth over time.
DeFi Interest Compounding
DeFi interest compounding leverages smart contracts to automatically reinvest earnings, significantly increasing returns compared to simple interest, which calculates returns solely on the principal amount. Compound interest in decentralized finance enhances capital growth exponentially by accruing interest on both the initial principal and the accumulated interest over time.
Simple Interest vs Compound Interest for calculating returns. Infographic
 moneydiff.com
moneydiff.com